数据流
数据流可以被视作一个长度为 d 的固定数组 A。随着后续数据的不断到达,数组 A 的长度或其中的元素都可能发生变换。
数据流子模型
根据数据流中数据对数组 A 的不同影响方式,可以划分为三个子模型。
- 时间序列模型:每个数据项 ai=A[i] 按照 i 增加的顺序出现,相等于时间序列。
- 收银机机模型:每个数据项 ai=(j,Ii)。其中 Ii≥0 表示对 A[i] 的增量。即 Ai[j]=Ai−1[j]+Ii0。如果有多个 ai,则表示在一段时间上 A[j] 的增量。
- 十字转盘模型:每个数据项 ai=(j,Ui)。其中 Ui 可正可负,表示对 A[i] 的更新。即 Ai[j]=Ai−1[j]+Ui。该模型适合表示数据流动态的出入状态。
根据数据流各元素的重要程度,可以划分为三个子模型。
令 t 为某一特定时间点,d 为当前时间点。
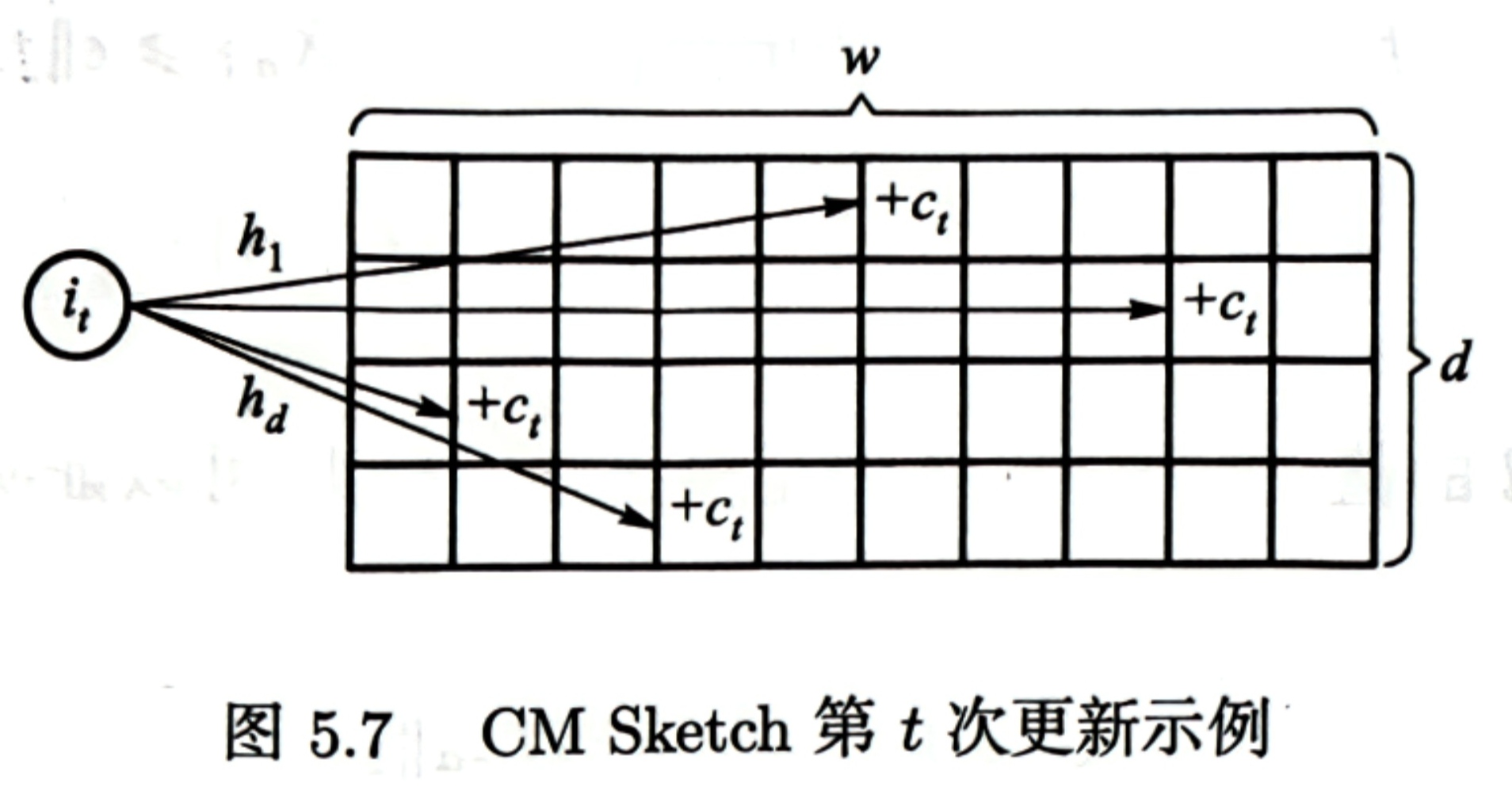
- 界标模型:起始点固定,终止点随着时间推移不断递增。范围:[t ... d−1]
- 滑动窗口模型:起始点和终止点都会随着时间推移同步递增。仅考虑最近的 W 个元素。范围:[max(0,d−W) ... d−1]
- 衰减窗口模型:新到达的元素,重要程度最高;旧的元素,重要程度较低。范围:[0 ... d−1]
近似算法
∣A(σ)−B(σ)∣<ϵB(σ) ∣A(σ)−B(σ)∣<ϵ - (ϵ,δ) 近似算法(相对误差)
Pr[∣A(σ)−B(σ)∣<ϵB(σ)]>1−δ - (ϵ,δ) 近似算法(绝对误差)
Pr[∣A(σ)−B(σ)∣<ϵ]>1−δ 频繁项挖掘
在数据流 σ=<a1,a2,...,am>,ai∈[n] 中,定义一个频数向量。
其中 n 为该数据流中不同元素的个数,fi 为元素 ai 的频数,且满足 ∑i=1nfi=m。
f=(f1,f2,...,fn) 缺陷:内存消耗巨大。只要数据流出现一个新的元素,内存就需要为其创建一个计数器。
求大多数
如果 ∃aj:fj>m/2,则输出 aj。
求频繁项
给定一个参数 k,输出频繁元素集合 {aj:fj≥m/k}。
或者,给定一个参数 ψ,输出频繁元素集合 {aj:fj>ψm}
确定性近似频数算法 Misra Gries
Misra Gries 算法和俄罗斯算法非常相似。
对输入的数据流 σ=<a1,a2,...,am>,ai∈[n],使用 k 个计数器,输出频繁元素集合 F。
算法流程:每当到达一个元素 am
- 如果已经为其创建了计数器,则相应计数器 +1。
- 如果没有相应计数器,则初始化新计数器为 1。
- 如果当前计数器个数为 k(满),则把所有计数器 −1,并删除值为 0 的计数器。
不足:
- Misra Gries 算法可能会出现误报。但频繁元素一定在最后的输出结果中。
- 输出结果对元素的频数无从知晓
随机近似频数算法 Count Sketch
Misra Gries 算法输出的结果中每个元素的频数无从知晓,而随机近似频数算法 Count Sketch 则可以估计频繁元素的频数。
简单抽样算法
核心思想:对于到达的元素 ai,以概率 p=M/n 对该元素的频数加 1。其中 M 表示抽样后的数据流大小,m 表示原数据流大小。
- 更新操作:当元素 ai 到达时,以 p 的概率更新 ci 的值。以 1−p 的概率保持 ci 的值不变。
- 估计元素频数操作:返回元素频数数组,其中每个元素的频数为 fˆi=ci/p。
不足:当数据流中的元素非常多时,该算法所需的计数器也随之增加。
定理:简单抽样算法成为 (ϵ,δ) 近似算法的空间需求是 M=O(mlog(1/δ)/ϵ2)。其中,m 为原数据流大小,ϵ 是误差因子,δ 是控制误差在一定范围的尾概率上界。
Basic Count Sketch 算法
Basic Count Sketch 算法维护一个计数数组 C 和两个哈希函数 h(a) 和 g(a)。
- h(a):将 n 个元素均匀的映射到 k 个位置上。
- g(a):将 n 个元素均匀的映射为 −1 或 +1。
- 对于查询元素 ai 估计除的频数为 faˆ=g(a)C[h(a)]。
Basic Count Sketch 算法的空间需求为 k=O(1/ϵ2δ),与数据流大小无关
Count Sketch 算法
使用 Tug of War 技术,能够在 k=O(ln(1/δ)/ϵ2) 时得到真实频数 ϵ,δ 的近似估计。
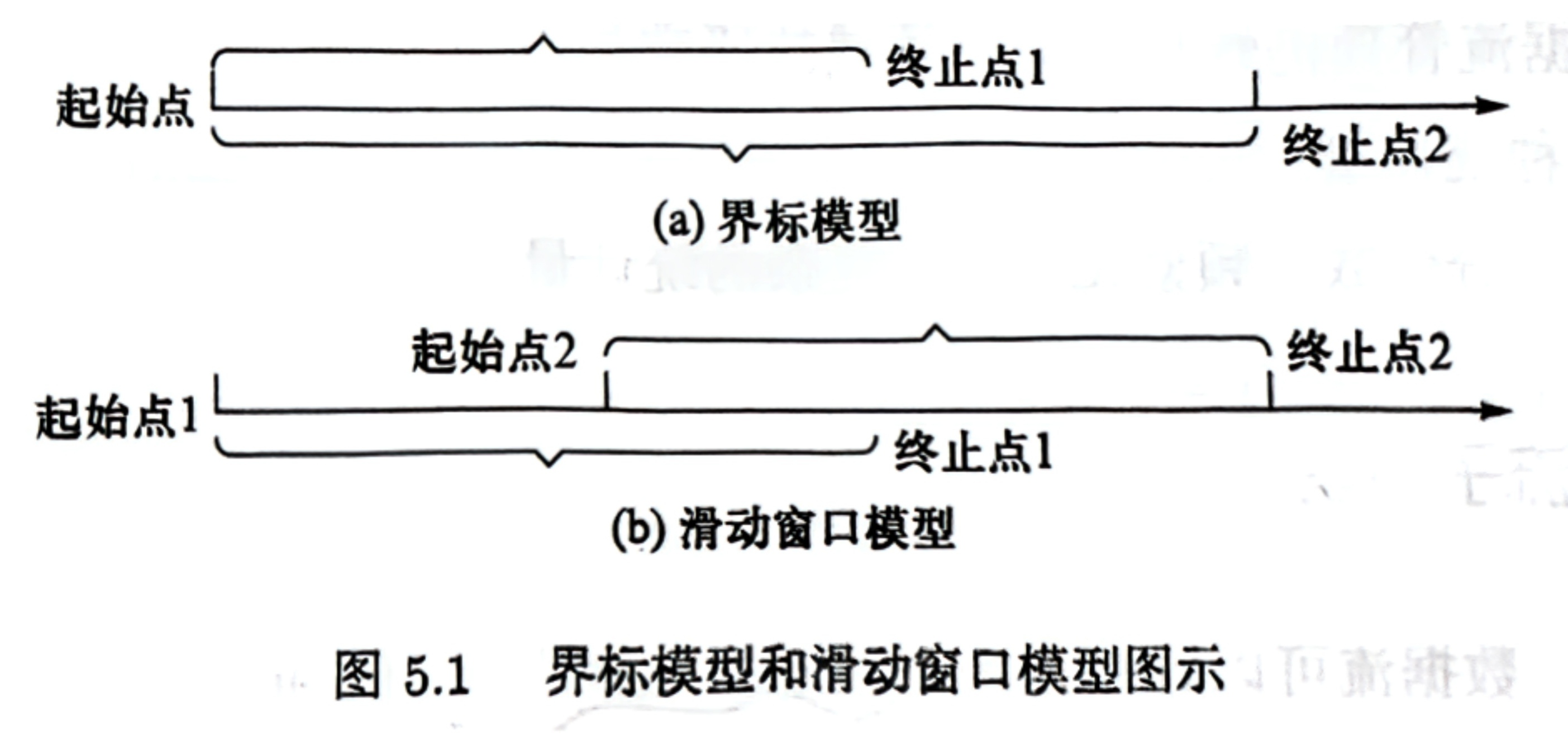
Count Sketch 算法核心思想:在 Basic Count Sketch 算法的基础上,将哈希函数的个数增加到 t 个,将每个元素都映射到 t 个位置上,再取 t 个位置上的频数估计的中位数。(t=log(1/δ))
Count Sketch 算法的精度只与 ϵ 和 δ 有关,与数据流规模大小无关。
Count-Min Sketch 算法
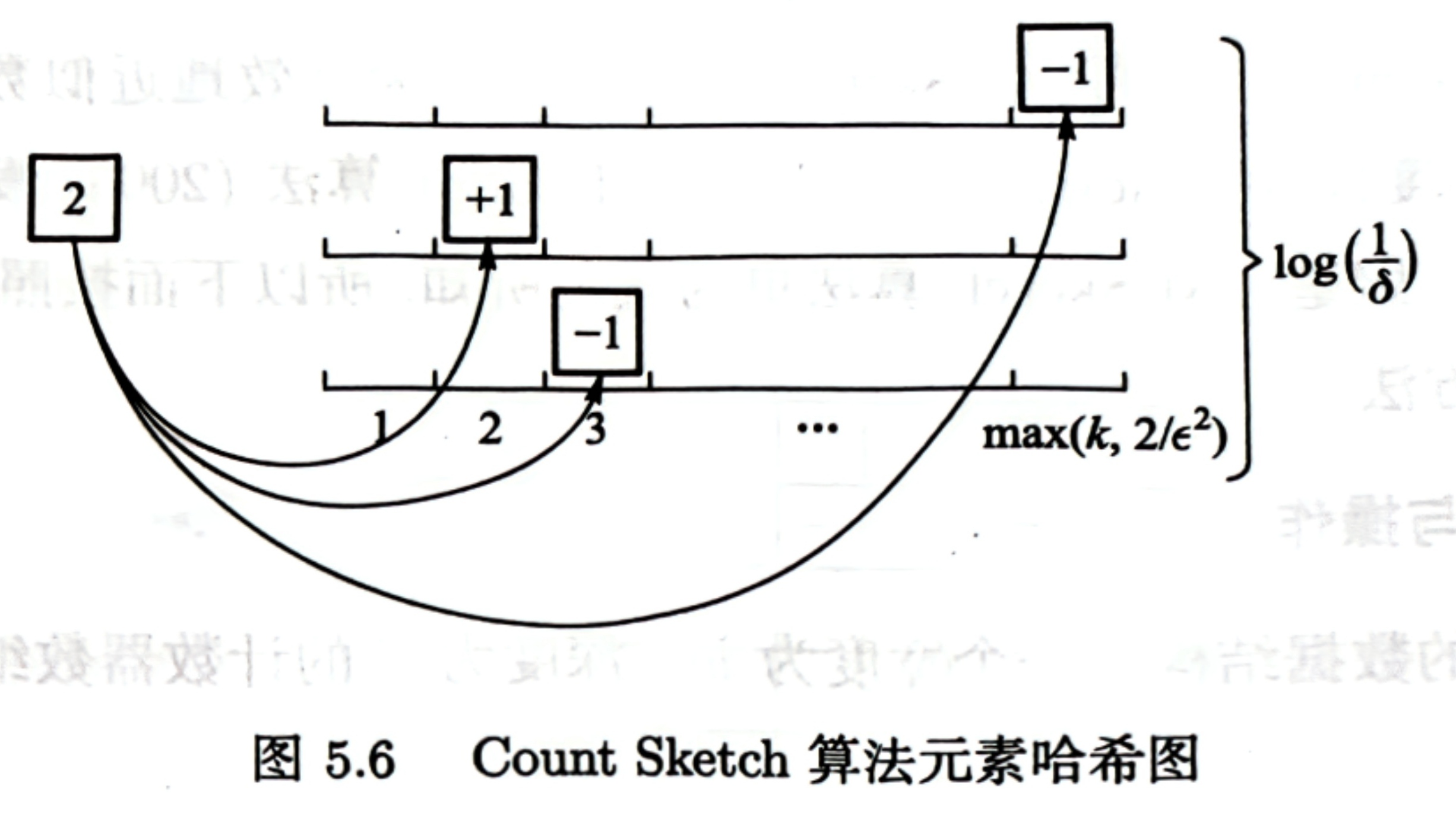
可以更为高效地近似数据流中的频数估计,它的复杂度仅为 O(log(1/δ)ϵ)。
CM Sketch 的数据结构是一个宽度为 w、深度为 d 的计数器数组。初始化时,每个元素都为 0,另外有 d 个哈希函数用于映射数据流到某个计数器中。算法返回的值为每行相应映射位置的最小值 fˆa=min1≤i≤dC[i][hi(a)]。